De rekenliniaal/rekenschijf is eeuwenlang een zeer gewaardeerd rekeninstrument geweest, dat in allerlei uitvoeringen zijn nut heeft bewezen. Het was vooral geliefd bij technici, want naast de mogelijkheid tot het uitvoeren van gecomplicerde berekeningen, is het ook mogelijk goniometrische waarden (verhoudingen) van hoeken, kwadraten en machtsverheffingen (3e) van getallen rechtstreeks af te lezen.
Daarom werd in andere vakgebieden, waar het rekenen niet alleen bestond uit "optellen" en "aftrekken" van getallen, er ook intensief mee gewerkt.
Wel moet nog even vermeld worden, dat juist het simpele "optellen" en "aftellen" bijna het enige is wat niet op de rekenliniaal uitgevoerd kan worden, gezien de logaritmische schaalverdelingen op de liniaal
Het kan wel via een omweg door toepassing van de formule a ± b =(a/b ± 1)b, maar deze omslachtige weg zal niemand in de praktijk gebruiken.
Een blik in een oude catalogus van "Aristo", een gerenommeerd Duits rekenliniaalmerk uit het verleden, toont een grote verscheidenheid aan modellen en de daaraan verbonden gebruiksmogelijkheden, bedoeld voor diverse vakgebieden.
Om u een indruk te geven noem ik hier wat vakgebieden: Landmeetkunde, Navigatie t.b.v. Scheepvaart en Luchtvaart, Handel, Betonconstructies, Electronica, Textielindustrie en Onderwijs.
"Voor het klassikaal onderwijs werden grote instructielinialen (ongeveer 1,5 m lang) gebruikt, die makkelijk aan een schoolbord konden worden opgehangen".
In de nadagen van het "echte" gebruik van de rekenliniaal zijn door meerdere firma's dia-series uitgebracht, die d.m.v. een diaprojector geprojekteerd konden worden en de instructie goed toonbaar maakte.
De klassieke rekenliniaal bestaat eigenlijk uit drie linialen met een logaritmische schaalverdeling. De bovenste en de onderste liniaal zijn met elkaar verbonden (het lichaam van de liniaal), met dien verstande dat de middelste liniaal (de tong) door gebruik te maken van gleuven in de twee andere linialen, verplaatst kan worden. Over het geheel is een doorzichtige verplaatsbare loper (cursor) geschoven. Op die loper zijn draadlijnen aangebracht, die gebruikt worden voor de instelling en de aflezing.
Sommige lopers zijn zelfs voorzien van een loep, zodat de instelling en aflezing gemakkelijker en exacter kan geschieden.
Werkingsprincipe:
Het werkingsprincipe is gebaseerd op het logaritmische stelsel van de Engelse wiskundigen Napier en Briggs (17e eeuw). Briggs heeft dit stelsel uitgewerkt met het getal 10 als grondtal.
Wanneer men nu twee linialen met een identieke lineaire schaalverdeling langs elkaar schuift, kan men in principe de vermelde waarden (uitgedrukt in getallen) optellen en/of aftrekken.
Brengt men echter inplaats van een lineaire schaalverdeling een logaritmische schaalverdeling op de linialen aan, (zie onderstaand figuur)
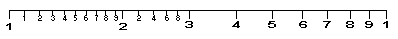
dan kan men dus door het naast elkaar verschuiven van deze linialen ook een optelling of aftrekking van de vermelde waarden maken en deze respectievelijk benutten voor de uitvoering van een vermenigvuldiging of een deling van de bij die waarden behorende getallen.
(Want log a + log b= log a×b en log a - log b= log a÷b).
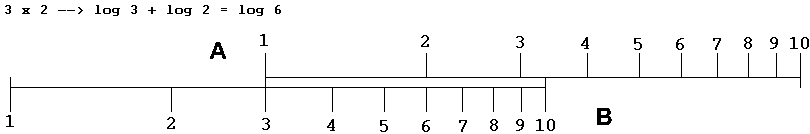
Wilt u op uw eigen p.c. dit voorbeeld of wat andere eenvoudige berekeningen uitproberen, maak dan gebruik van de mogelijkheid die de website van de firma Sagmilling u biedt.
De te bereiken nauwkeurigheid van de berekeningen, die men met een rekenliniaal kan bereiken is van verschillende factoren afhankelijk, maar men moet in eerste instantie het doel van het eindresultaat goed inschatten. Men moet zich goed realiseren, dat de getallen waarmee men technische berekeningen uitvoert meestal door metingen verkregen zijn. Daaruit volgt dat de gevonden getallen benaderingen zijn, ondanks het gebruik van de meest verfijnde meetinstrumenten.
Aan de hand daarvan kunnen de afrondingen van de te gebruiken variabelen vastgesteld worden.
Om bepaalde berekeningen nog nauwkeuriger te kunnen uitvoeren heeft men een wat langere liniaal (50 cm) gefabriceerd, zodat de instelling en de aflezing, door een "fijnere" schaalverdeling, nauwkeuriger kan geschieden.
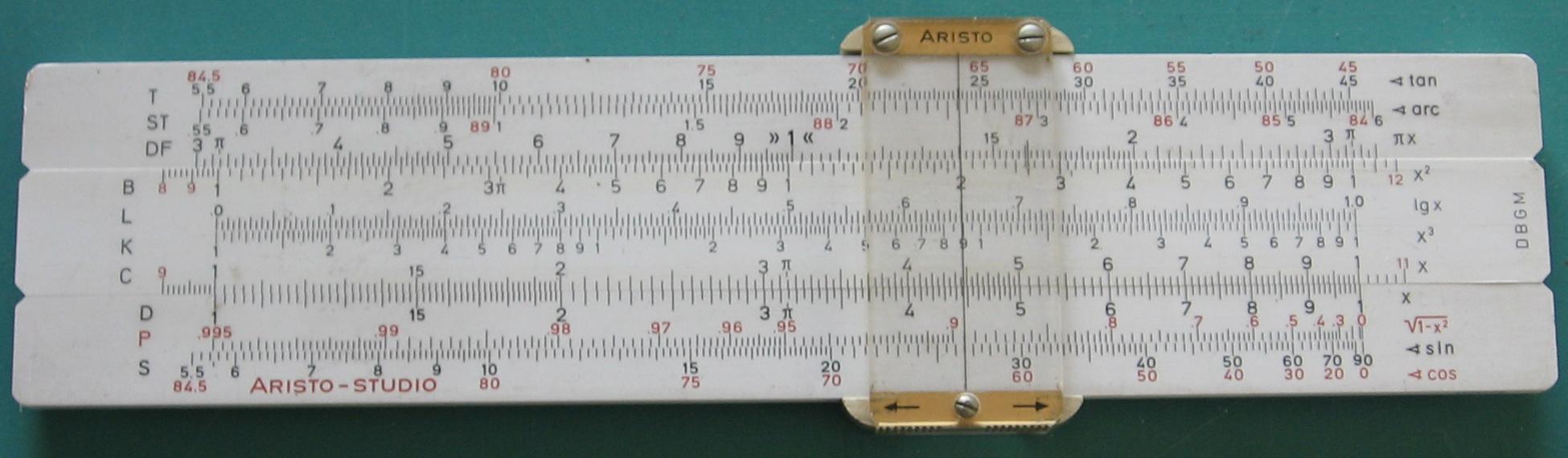
Wilt u zich serieus verdiepen in het gebruik en de mogelijkheden van de rekenliniaal, dan vind ik, naast de wat summiere door de fabrikanten bijgeleverde gebruiksaanwijzingen, de volgende studieboeken duidelijke gidsen:
